this post was submitted on 23 Aug 2023
67 points (100.0% liked)
196
18015 readers
682 users here now
Be sure to follow the rule before you head out.
Rule: You must post before you leave.
Other rules
Behavior rules:
- No bigotry (transphobia, racism, etc…)
- No genocide denial
- No support for authoritarian behaviour (incl. Tankies)
- No namecalling
- Accounts from lemmygrad.ml, threads.net, or hexbear.net are held to higher standards
- Other things seen as cleary bad
Posting rules:
- No AI generated content (DALL-E etc…)
- No advertisements
- No gore / violence
- Mutual aid posts are not allowed
NSFW: NSFW content is permitted but it must be tagged and have content warnings. Anything that doesn't adhere to this will be removed. Content warnings should be added like: [penis], [explicit description of sex]. Non-sexualized breasts of any gender are not considered inappropriate and therefore do not need to be blurred/tagged.
If you have any questions, feel free to contact us on our matrix channel or email.
Other 196's:
founded 2 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
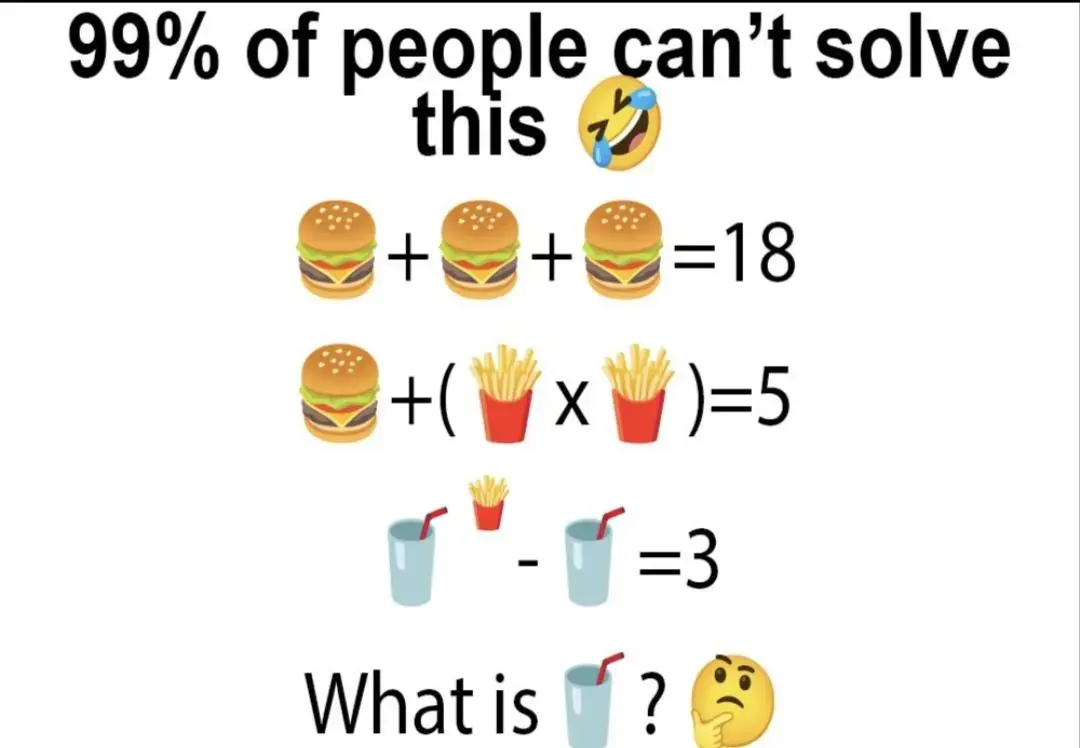
Well let's break it down:
Simple!
Wait, what happened in the second to last bullet point? You can't convert a power like that when subtracting (you can when dividing).
It's like you'd convert "2^4 - 2" into "2^(4-1)", which gives two different results (14 vs 8).
For those curious, I threw 🥤^i - 🥤 = 3 into wolfram.
🥤 ≈ -2.97983 + 0.0388569 i... or 🥤 ≈ 0.27972 - 0.748461 i...
You're right, idk what I was thinking there 😕
I think they're saying no one can give the real answer to this... which is technically true because the answer is imaginary.
Bah, yes I forgot about that
Don't you mean 🍟 = i?
And just like that, I'm back to junior high grumbling about the concept of imaginary numbers.
Fuck you, y'all made up! 🤣
Lol I didn't quite get my math right, but it still involves imaginary numbers. Fun fact! Any 3D game you've played in the past probably quarter century doesn't just use 1 dimension of imaginary numbers, but 3 to represent 3D rotation! Quaternions are difficult to visualize since it's a 4-dimensional quantity but they're perfect for representing rotation in 3D space without suffering from gimbal lock like rotation matrices.