@mau @matematica C'è qualcosa che non mi torna, di numeri primi di quella forma ce ne sono, per esempio 140001089, 1401099989 e 14000109989.
Ma poi 57p si intende 57 seguito dalla stringa delle cifre di p oppure è una moltiplicazione?
this post was submitted on 27 Aug 2025
1 points (100.0% liked)
Matematica
94 readers
1 users here now
Benvenuti alla comunità dedicata alla regina delle scienze: la matematica!
Vi ricordiamo di dare un'occhiata alla Guida all’utilizzo di Feddit
Ovviamente vi raccomandiamo di proporre link a tema, in italiano ma anche in inglese. In quest'ultimo caso postate il link con il suo titolo originale non tradotto, mentre per il testo potete tranquillamente pubblicare una sintesi in italiano. Ovviamente non sono ammessi articoli che rimandano alla pseudoscienza o che non hanno attinenza con la matematica.
founded 2 years ago
MODERATORS
@enzotib
Infatti nella lista OEIS ci sono
7980062073 = 57·140001089;
79862699373 = 57·1401099989; e
798006269373 = 57·14000109989.
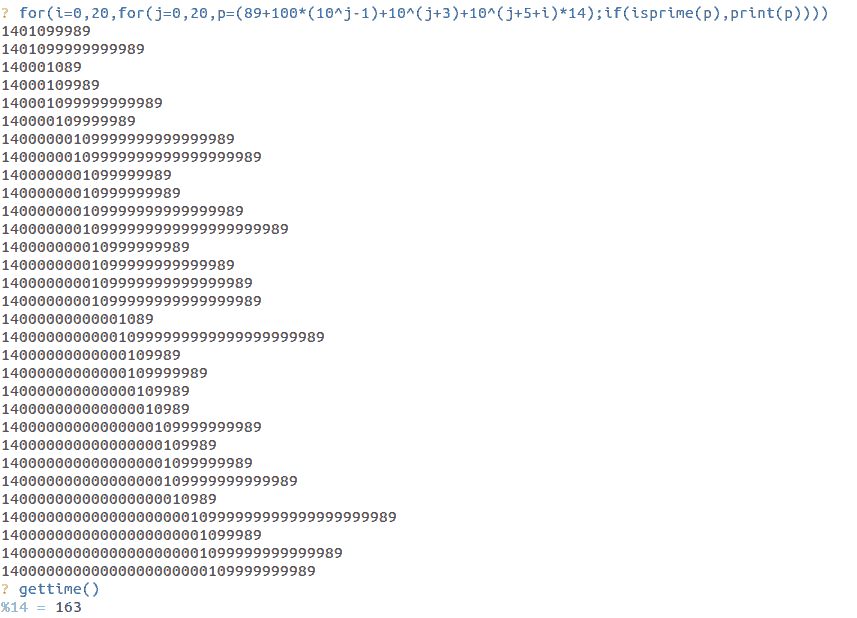
Per altro la seguente riga per GP-Pari[*]
for(i=0,20,for(j=2,22,p=11*(10^j-1)+14*10^(j+3+i);if(isprime(p),print(p))))
ne ha trovati una trentina in 163 millisecondi.
Magari non è facile dimostrare che non ce ne sono altri in mezzo tra i sette della lista OEIS e quelli che si possono trovare in questo modo…
[*] https://pari.math.u-bordeaux.fr/
@mau @matematica
@enzotib io sono partito da https://jlpe.tripod.com/ppn/ppn.htm . Ma che c'entrano i numeri primi? È vero che avevo sbagliato a fare l'esempio (ora è corretto), ma l'unico divisore proprio di 140001089 è 1 e quindi la somma dei divisori scritti alla rovescia è 1, non 980100041.
57p è una moltiplicazione.